Verrouillage de phase sans verrouillage de fréquence
vendredi 2 septembre 2011 à 00:00Ceci est la traduction en français de mon article publié dans Physical Review Letters, au sujet de la synchronisation assistée par résonance dans des oscillateurs couplés : verrouillage de phase sans verrouillage de fréquence.
Auteurs : Jérémie Boudah Thévenin (Moi), Marco Romanelli, messieurs Marc Vallet et Marc Brunel (mes encadrants de thèse), ainsi que Thomas Erneux.
Résumé : nous démontrons expérimentalement le verrouillage de phase sans verrouillage de fréquence de deux oscillateurs non-linéaires couplés. Ce régime de synchronisation est obtenu pour deux modes couplés d'un laser, au-delà de la plage de verrouillage de phase déterminée par l'équation d'Adler, grâce à un mécanisme de résonance. Spécifiquement, nous montrons que les amplitudes de ces deux modes laser fluctuent fortement ce qui provoque la synchronisation de fréquence moyenne, même si les phases instantanées ne sont pas verrouillées. Nous présentons également un modèle théorique qui est en accord avec nos observations expérimentales.
Introduction
La synchronisation, c'est à dire la capacité qu'ont deux oscillateurs couplés d'osciller à la même fréquence, est une propriété répandue voire omniprésente dans la nature, qui apparait tant dans les horloges biologiques, les réactions chimiques, les oscillateurs mécaniques ou électrique, que dans les lasers; juste pour mentionner quelques exemples bien connus [1]. Quand l'amplitude des oscillations est constante, les deux oscillateurs couplés peuvent être décrit par une unique équation pour leur phase relative Φ :
Où ∆ν est le désaccord entre les fréquences des deux oscillateurs et fA est la constante de couplage exprimé sous forme de fréquence. L'équation (1) fut originellement développée par Adler [2] pour un oscillateur électrique asservi à une référence externe et qui a prouvé depuis son utilité dans une large variété de situations. De récents exemples incluent des oscillateurs biologiques [3], la dynamique d'excitation des micro-particules de détection [4], ou les lasers à point quantique injectés [5]. L'équation d'Adler montre que le comportement de deux oscillateurs couplés dépend du ratio entre ∆ν et fA. Si |∆ν/fA| ≤ 1, une solution stable et stationnaire existe pour l'équation (1). A contrario, si |∆ν| excède fA, les deux oscillateurs ne peuvent se synchroniser et leur phase relative croit indéfiniment au cours du temps.
L'équation d'Adler se vérifie bien, dans la limite d'un faible couplage et d'un faible désaccord, pour les lasers couplés de classe A [6]. D'un autre coté, les investigations théoriques sur les lasers de classe B injectés [7, 8] pointent du doigt que l'équation (1) devrait également inclure la dynamique d'amplitude. De cette complexité dynamique accrue résulte l'existence d'un régime intermédiaire entre le verrouillage de phase et la dérive de phase (déverrouillage). Dans ce régime, appellé entrainement de phase, la phase relative n'est pas stationnaire; cependant, elle reste bornée. Cela signifie que les fréquences moyennes des oscillateurs sont verrouillées. Bien que l'entrainement de phase, c'est à dire le verrouillage de fréquence sans verrouillage de phase, est un genre de synchronisation universel (prédit par exemple pour les oscillateurs de Van der Pol couplés [9]), aucune preuve expérimentale de ce comportement n'a été rapportée, probablement parce qu'une claire discrimination par rapport au verrouillage de phase standard est délicate. Dans cette lettre, nous montrons que les lasers constituent un support expérimental pratique pour révéler cette dynamique d'entrainement de phase. Nous avons mesuré la phase optique entre deux champs laser couplés et trouvé qu'elle était bornée, c'est à dire que les fréquences moyennes des champs étaient synchronisées, au-delà de la limite de verrouillage de phase prédite par l'équation d'Adler. Notre observation expérimentale est fortement liée à l'existence d'une échelle de temps intrinsèque TR = 1/fR, caractéristique de la dynamique des lasers de classe B, où fR est la fréquence des oscillations de relaxation [6]. Nous avons trouvé que la synchronisation s'étend au-delà de la limite d'Adler quand les deux échelles de temps gouvernant la dynamique des lasers de classe B couplés, c'est à dire TR et T1 = 1/∆ν sont proches. Près de la résonance, les champs laser sont très sensibles au couplage, avec pour résultat que la synchronisation des fréquences moyennes est observée pour un couplage faible.
Montage expérimental
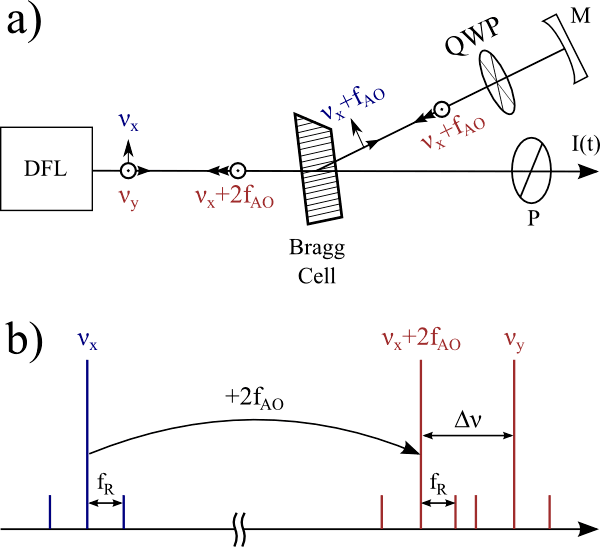
FIG 1. (a) Schéma expérimental. Un laser bi-fréquence (DFL) émet deux champs laser mono-modes, polarisés perpendiculairement, νx et νy. Le champ x est réinjecté dans le champ y après que sa fréquence soit augmentée de 2fAO et que sa polarisation soit tournée par une lame quart-d'onde (PR). Le signal de battement I(t) est détecté derrière un polariseur (P). (b) Schéma des fréquences impliquées. Le champ x et ses bandes d'oscillations de relaxation situées à ± fR sont décalés en fréquence de manière à être quasi-résonants avec le champ y.
Notre montage expérimental est décrit sur la figure 1(a). On utilise un laser à état solide bi-fréquence pompé par diode (laser Nd3+:YAG émettant à la longueur-d'onde de 1064 nm). Ce type de lasers nous donnent deux champs lasers monomode accordables en fréquence, correspondant aux deux modes propres de polarisation de la cavité laser [10]. L'élément-clé de ce système dans le contexte présent est que la différence de fréquence ∆ν0 = νy – νx des champs lasers “en boucle ouverte” Ex et Ey est intrinsèquement très stable, les deux champs lasers étant définis par la même cavité optique. Mieux encore, ∆ν0 est précisément accordable est usant d'un élément bi-réfringent intra-cavité (non-montré ici), nous permettant d'explorer le régime de faible désaccord de fréquence proche de fR. On choisit ∆ν0 = 200 MHz afin d'éliminer les effets cohérents de saturation croisée dans le milieu actif ; sous cette condition, chaque champ laser interagit avec son propre réservoir d'inversion de population [11]. Les deux champs lasers sont couplés optiquement par une cavité de réinjection contenant une cellule de Bragg qui décale la fréquence optique diffractée d'une quantité fAO [12], et une lame quart-d'onde qui fait basculer la polarisation x sur la polarisation y après réflexion sur le miroir de réinjection. La fréquence de commande du Bragg fAO est accordable autour de 100 MHz. Il en résulte que le champ polarisé suivant x est réinjecté sur le champ polarisé suivant y, décalé d'une quantité 2fAO. Le désaccord ∆ν est alors défini par ∆ν = ∆ν0 - 2fAO. La figure 1(b) dépeint les fréquences pertinentes pour notre système, parmi lesquelles on trouve la fréquence des oscillations de relaxation fR. La puissance optique réinjectée (~ 10–5 de la puissance d'un mode laser) est fixée de telle sorte que la largeur de la plage d'accrochage est fA = 0,8 fR, avec fR = 70 kHz.

FIG 2. (a), (b) Séries temporelles expérimentales de I(t), for ∆ν = 0,85 fR et ∆ν = 0,85 fR, respectivement. (c), (d) Séries temporelles correspondantes de I(t) obtenues par intégration numérique des équations (2)–(5).
Quand ∆ν ≈ fR, le champ x, décalé en fréquence et basculé en polarisation, excites le champ y de manière résonante. En conséquence, d'importantes fluctuations apparaissent dans les séries temporelles du signal de battement I(t) = |Ex + Ey|2. Pour l'illustrer, nous montrons une série temporelle d'un régime auto-impulsionnel se produisant pour ∆ν = 1,05 fR [Fig. 2(a)], et une série temporelle chaotique se produisant pour ∆ν = 0,85 fR. Des instabilités similaires d'intensité ont suscité beaucoup d'intérêt et ont été rapportée en détail [13, 14]. Cependant, la dynamique de la phase relative quand l'intensité devient instable a reçu une attention moindre. Dans notre dispositif nous avons un accès aisé à la phase relative optique. À cette fin, on fait interférer les champ x et y sur une photodiode rapide placée derrière un polariseur. Si le champ y est verrouillé à la fréquence νx + 200 MHz, on s'attend à ce que le signal de battement I(t) contienne une oscillation rapide à 200 MHz, verrouillée en phase avec la seconde harmonique du signal RF appliqué à la cellule de Bragg. L'oscillation à 200 MHz sera fortement, mais comparativement très lentement, modulée par les fluctuations d'intensité se déroulant sur un temps beaucoup plus long ~ TR. Ainsi, la mesure de la phase Φ du signal d'interférence, relative à la phase de la seconde harmonique du signal RF, nous donne accès à la phase du champ y relative à celle du champ x réinjecté. En utilisant un oscilloscope numérique rapide (40 GS/s), nous pouvons calculer l'histogramme la phase relative Φ entre le signal issu de la photodiode et le générateur RF. Les données brutes sont présentées fig. 3. Chaque mesure de la phase Φ est obtenue en mesurant la valeur moyenne sur 100 périodes, c'est à dire pour une trace temporelle de 500 ns (100 / 200 MHz) ; chaque histogramme contient 5000 mesures de la phase. La figure 3(a) montre un histogramme de la phase quand ∆ν = 0,3 fA, à l'intérieur de la plage d'accrochage d'Adler. On obtient un pic relativement étroit, dont la largeur est en accord avec la dérive de fréquence du champ laser mesurée indépendamment, et qui vaut 0,4 kHz/s. Ce bruit est dû à des artefacts techniques (dérives mécanique ou provenant des fluctuations de la puissance de pompe). Pour ∆ν = 2 fA, bien en-dehors de la plage d'accrochage d'Adler, la dérive de la phase relative Φ induit un histogramme plat [3(b)]. Enfin, quand ∆ν = 1,33 fA, en dehors de la plage d'accrochage d'Adler, on obtient un histogramme de la phase plus large que [3(a)], mais la phase relative reste cependant bornée dans un intervalle plus petit que [–π; π] [3(c)], ce qui indique qu'une synchronisation se produit au-delà de fA. Cet histogramme est cohérent avec l'hypothèse d'une phase dépendante du temps, mais bornée, qui est le comportement théoriquement attendu, comme nous le montrons ci-après. Il est important de noter que cette dynamique de phase bornée n'apparait que pour d'importante fluctuations d'intensité [voir la figure 3(d), présentant la série temporelle de I(t) et la densité spectrale de puissance correspondante]. La phase bornée est même observée quand l'intensité devient chaotique, comme dans la figure 2(b).
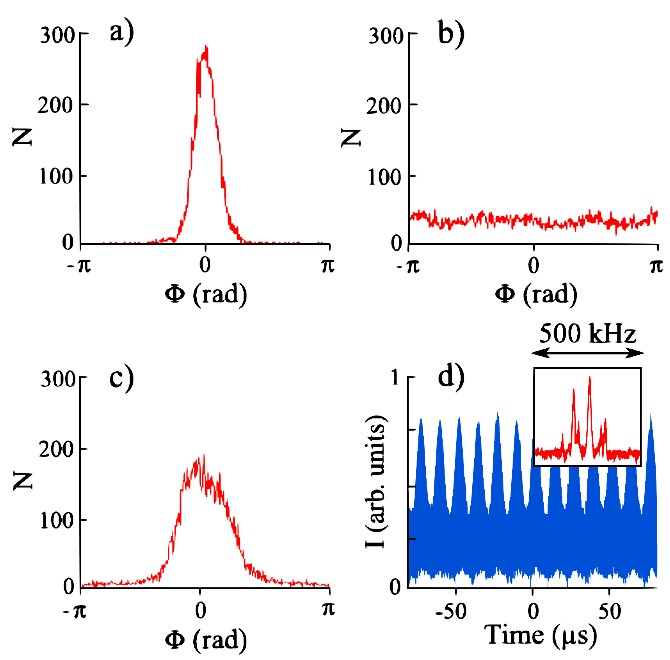
FIG 3. Histogrammes de la phase Φ pour (a) ∆ν = 0,3 fA, (b) ∆ν = 2 fA, (c) ∆ν = 1,33 fA. Le centre des histogrammes a été taré par soucis de clareté. (d) Série temporelle de I(t) correspondant à l'histogramme (c). En insert : densité spectrale de puissance de I(t) centré sur 200 MHz.
Modèle théorique
Ces découvertes expérimentales sont à comparer aux prédictions du modèle bi-mode d'équations de population [10]. Une équation de type Adler peut être formulée pour la phase relative Φ des champs sous la forme :
À la différence de l'équation (1), ici la dynamique de phase dépend des amplitudes des oscillateurs. L'équation (2) doit être accompagnée des équations pour les intensités Ix, Iy et pour les réservoirs d'inversion de population Nx,Ny (associés aux états propres x et y du laser) :
Dans les équations (2)–(5), les dérivées temporelles se rapportent à un temps sans dimension rapporté au temps de vie des photons dans la cavité laser tc = 4,4 ns ; ε = tc / tp = 3,9 × 10–5, où tp est la demie-vie de l'inversion de population ; r = 1,2 est le taux de pompage : fA = √R3 / 2π = 5 × 10–4 est le paramètre de couplage ramené à une fréquence (qui est également la largeur de la plage d'accrochage d'Adler), avec R3 la réflectivité de la cavité de réinjection (l'efficacité de diffraction de la cellule de Bragg est contenue dans R3); β = 0,6 tient compte la saturation croisée dans le milieu actif. Du fait que le temps d'aller-retour dans la cavité de réinjection (3,3 ns) est beaucoup plus court que TR (14 µs), on peut considérer que la réinjection est immédiate. Nous avons également vérifier numériquement que les équations (2)–(5), incluant ce délai, produisaient les même résultats. Toutes les valeurs des paramètres sont déterminées expérimentalement ; aucun paramètre de notre modèle n'est posé arbitrairement. Comme on peut le voir dans la figure 2, l'intégration numérique des équations (2)–(5) reproduit bien la dynamique d'intensité du laser [Fig 2(c) et 2(d)].
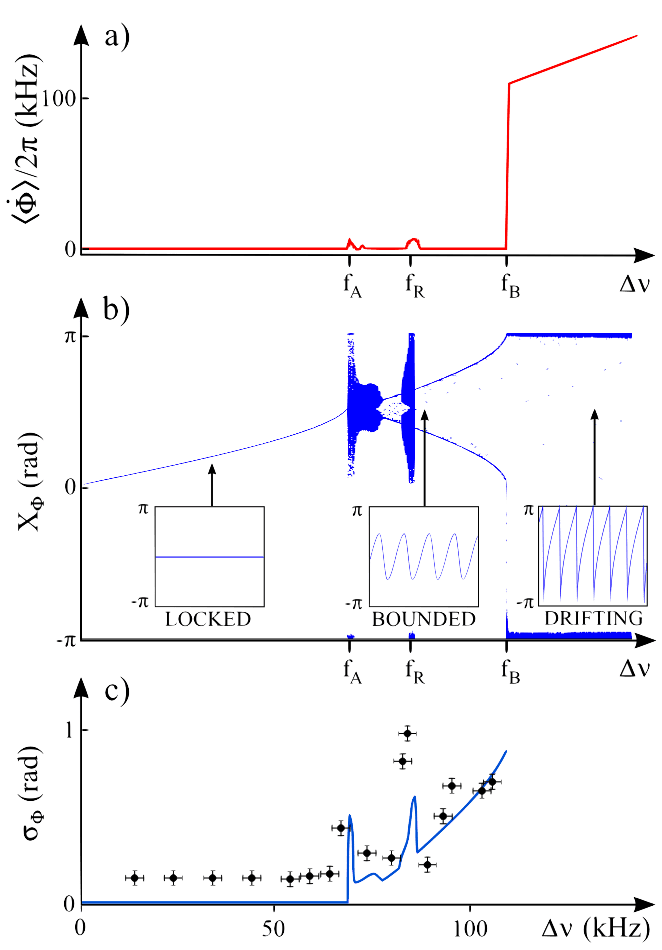
FIG 4. (a) Diagramme de ⟨dΦ/dt × 1/2π⟩ versus ∆ν, obtenu par intégration numérique des équations (2)–(5).
La comparaison entre le modèle et l'expérience pour la dynamique de la phase est résumée dans la figure 4. Dans la figure 4(a), nous présentons la différence de fréquence moyenne calculée ⟨dΦ/dt × 1/2π⟩ en fonction de ∆ν. Pour O ≤ ∆ν ≤ fA, ⟨dΦ/dt⟩ = 0, c'est qui signifie que les deux fréquences sont verrouillées. Cette région correspond à la plage d'accrochage d'Adler. On voit qu'un région où ⟨dΦ/dt⟩ = 0, c'est à dire où les deux oscillateurs sont synchronisés, existe au-delà de fA, jusqu'à une fréquence que nous notons fB. Seules deux petites portions de cette région, autour de fA et fR, ne sont pas rigoureusement verrouillées. Pour aller plus loin, nous regardons les extrema de la phase XΦ de Φ(t), en fonction de ∆ν [Fig. 4(b)]. Nous observons le comportement suivant : tant que ∆ν ≤ fA, une solution stationnaire stable existe et le verrouillage de phase est atteint ; pour fA ≤ ∆ν ≤ fB, aucune solution stationnaire n'existe, Φ(t) oscille mais reste bornée, avec parfois des épisodes chaotiques, si bien que la verrouillage de fréquence persiste au-delà de la plage d'accrochage d'Adler fA jusqu'à fB. Pour finir, quand ∆ν ≥ fB, la phase Φ(t) dérive indéfiniment, et les deux oscillateurs ne sont plus synchronisés. Nous insistons sur le fait que dans la figure 4(b) les extrema de la phase Φ ne sont pas calculés sur la phase “déroulée” : Φ(t) est restreinte à l'intervalle [–π; π], ce qui a pour conséquence qu'une phase dérivante, non-bornée, parait être un signal en dent-de-scie, avec d'abrupts sauts verticaux au moment où Φ(t) atteint π [voir l'insert de la figure 4(b)]. On voit donc, pour ∆ν ≥ fB, des extrema locaux à –π et π alors que la phase n'est pas bornée. Dans la figure 4(c) nous comparons la valeur mesurée de l'écart-type σΦ de Φ à la valeur calculée à partir de notre modèle, en fonction de ∆ν. Les points expérimentaux sont calculés à partir d'histogrammes comme ceux de la figure 3. Notre modèle produit histogramme à deux pics pour la phase bornée [Fig. 4(b)], mais nous avons vérifié numériquement que cette structure disparait si on prend en compte la présence du bruit révélé par la figure 3(a). La théorie et l'expérience sont en bon accord ; la tendance générale de la courbe théorique est bien reproduite, de même que le comportement autour de fA et fR. L'existence et les limites de la synchronisation des fréquences moyennes au-delà de la plage d'accrochage d'Adler est clairement mis en évidence. Notons qu'aucun point expérimental ne figure au-delà de fB, simplement parce que les histogrammes sont alors comme dans la figure 3(b). Cela est cohérent avec le modèle. Dans la figure 4, les trois valeurs particulières fA, fR et fB du désaccord de fréquence apparaissent. Tout d'abord, l'étroite plage de déverrouillage autour de fA est due à la présence de saturation croisée entre les deux champs laser. Si β est posé égal à 0 dans le modèle, la transition du verrouillage de phase à la phase bornée se déroule continument via une bifurcation de Hopf, et la synchronisation est conservée au voisinage de fA. Deuxièmement, il est compréhensible qu'au voisinage de la résonance fR il existe une autre plage étroite de déverrouillage, car les fluctuations d'intensités sont importantes pour que le système garde sa stabilité. Enfin, concernant fB, nous notons que, contrairement à fA, ce n'est pas un point de bifurcation, mais cela correspond presque à la valeur pour laquelle la trajectoire de champ Ey dans le plan complexe entoure le point 0 [8].
Conclusions
En conclusion, nous avons démontré l'existence d'une région de synchronisation au-delà de la limite fA de l'équation d'Adler. De ce que nous en avons, cela constitue la première démonstration expérimentale d'un verrouillage de fréquence sans verrouillage de phase dans une paire d'oscillateurs couplés. Nous avons montré qu'entre fA et fB, où le verrouillage de phase n'est pas possible, les deux oscillateurs sont néanmoins capables de maintenir le verrouillage de phase. L'équation (2) offre une interprétation heuristique de ce phénomène : quand ∆ν > fA, le couplage lui-même n'est pas suffisant pour verrouiller en phase les oscillateurs. Comme ∆ν est proche de fR, la résonance augmente effectivement le couplage et restaure la synchronisation via les fortes fluctuations des amplitudes des oscillateurs. Expérimentalement, quand fA > fR, de telle sorte qu'aucune résonance n'est disponible en dehors dans la plage d'accrochage d'Adler, nous n'avons trouvé aucune preuve d'une dynamique de phase bornée. Cela confirme le rôle essentiel de la résonance dans l'établissement de la synchronisation.
Pour les études à venir, une charactérisation expérimentale et théorique systématique du comportement du système en fonction du désaccord et de l'intensité réinjectée (sur plusieurs ordres de grandeur) est souhaitable, dans le but de chercher d'autres régions de l'espace des paramètres où une phase bornée peut être observée. En effet, il est connu qu'une quantité suffisamment grande de lumière injectée dans le laser peut être une source d'oscillations et d'instabilités de l'intensité du laser, même quand ∆ν est dans la plage d'accrochage [15]. Les prédictions théoriques actuelles de dynamiques de phase bornée se rapportent précisément à ce régime de “couplage fort” [7, 8, 16], où les instabilités sont guidées par la quantité de signal injecté plutôt que par la résonance du système. Au contraire, aucune analyse théorique de la dynamique de phase n'existe pour le moment pour un régime de “couplage intermédiaire” [8] où fA ≈ fR. Pour finir, notons que nos observations peuvent être pertinentes pour les lasers à semi-conducteurs également, et trouver des applications pour les gyro-lasers à état solide [17]. Il pourrait également être intéressant d'observer l'effet d'un couplage résonnant retardé [18].
Remerciements
Ce travail a été en partie financé par Rennes Métropole et le Conseil Général de Bretagne.
Références
- Arkady Pikovsky, Michael Rosenblum, and Jürgen Kurths, Synchronization: A universal concept in nonlinear sciences (Cambridge University Press, Cambridge, England, 2001).
- Robert Adler, A study of locking phenomena in oscillators, Proceedings of the IRE 34, 351 (1946).
- Raymond E. Goldstein, Marco Polin, and Idan Tuval, Noise and Synchronization in Pairs of Beating Eukaryotic Flagella, Physical Review Letters 103, 168103 (2009).
- Francesco Pedaci, Zhuangxiong Huang, Maarten van Oene, Stephane Barland, and Nynke H. Dekker, Excitable particles in an optical torque wrench, Nature Physics 7, 259 (2010).
- D. Goulding, S.P. Hegarty, O. Rasskazov, S. Melnik, M. Hartnett, G. Greene, J.G. McInerney, D. Rachinskii, and G. Huyet, Excitability in a Quantum Dot Semiconductor Laser with Optical Injection, Physical Review Letters 98, 153903 (2007).
- Thomas Erneux and Pierre Glorieux, Laser Dynamics (Cambridge University Press, Cambridge, England, 2010).
- Peter A. Braza and Thomas Erneux, Constant phase, phase drift, and phase entrainment in lasers with an injected signal, Physical Review A 41, 6470 (1990).
- M.K. Stephen Yeung and Steven H. Strogatz, Nonlinear dynamics of a solid-state laser with injection, Physical Review E 58, 4421 (1998).
- Tapesh Chakraborty and Richard H. Rand, The transition from phase locking to drift in a system of two weakly coupled van der pol oscillators, International Journal of Non-Linear Mechanics 23, 369 (1988).
- Jérémie Thévenin, Marc Vallet, Marc Brunel, Hervé Gilles, and Sylvain Girard, Beat-note locking in dual-polarization lasers submittedto frequency-shifted optical feedback, Journal of Optical Society of America B 28, 1104 (2011).
- Kenju Otsuka, Paul Mandel, S. Bielawski, D. Derozier, and Pierre Glorieux, Alternate time scale in multimode lasers, Physical Review A 46, 1692 (1992).
- Luc Kervevan, Hervé Gilles, Sylvain Girard, and Mathieu Laroche, Beat-note jitter suppression in a dual-frequency laser using optical feedback, Optics Letters 32, 1099 (2007).
- J.R. Tredicce, F.T. Arecchi, G.L. Lippi, and G.P. Puccioni, Instabilities in lasers with an injected signal, Journal of Optical Society of America B 2, 173 (1985).
- Åsa Marie Lindberg, Thomas Fordell, and Simo Valling, Dynamics, bifurcations and chaos in coupled lasers, Philosophical Transactions of the Royal Society A 366, 427 (2008).
- Stefan Eriksson and Åsa Marie Lindberg, Periodic oscillation within the chaotic region in a semiconductor laser subjected to external optical injection, Optics Letters 26, 142 (2001).
- S. Wieczorek, B. Krauskopf, T.B. Simpson, and D. Lenstra, The dynamical complexity of optically injected semiconductor lasers,Physics Reports 416, 1 (2005).
- Sylvain Schwartz, Gilles Feugnet, Philippe Bouyer, Evguenii Lariontsev, Alain Aspect, and Jean-Paul Pocholle, Mode-Coupling Control in Resonant Devices: Application to Solid-State Ring Lasers, Physical Review Letters 97, 093902 (2006).
- H.-J. Wünsche, S. Bauer, J. Kreissl, O. Ushakov, N. Korneyev, F. Henneberger, E. Wille, H. Erzgräber, M. Peil, W. Elsäßer, and I. Fischer, Synchronization of Delay-Coupled Oscillators: A Study of Semiconductor Lasers, Physical Review Letters 94, 163901 (2005).